What Is A Geopotential Height And Why Is It So Useful?
Jan 2, 2021 4:54:58 GMT -6
HarahanTim-Now in Gallatin, TN, SKYSUMMIT, and 2 more like this
Post by thermalwind - Touro on Jan 2, 2021 4:54:58 GMT -6
Warning: There be math ahead, but I'm going to keep it simple as I can.
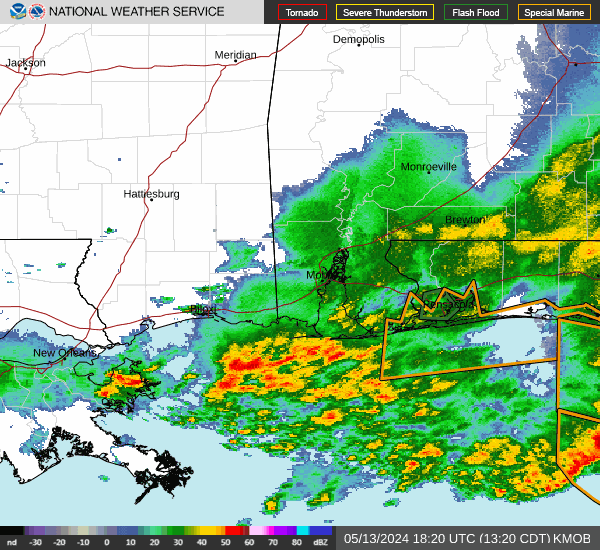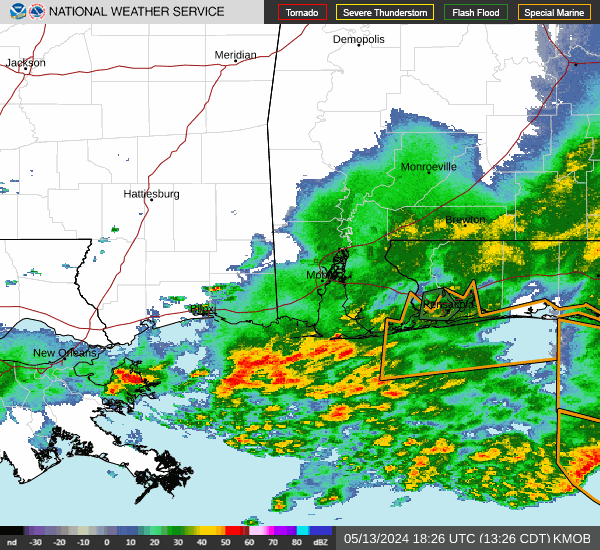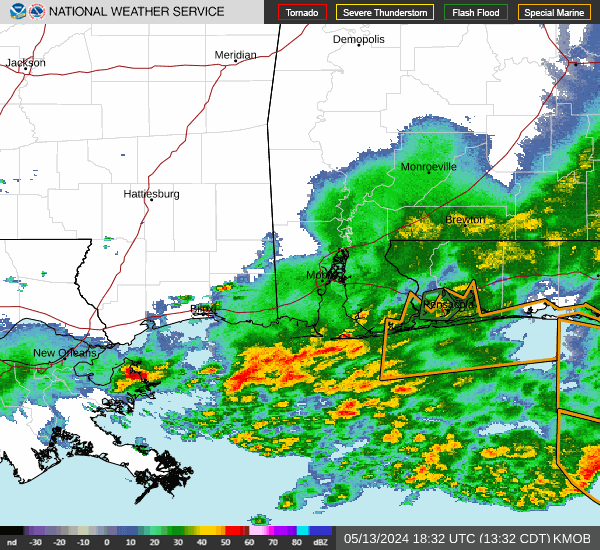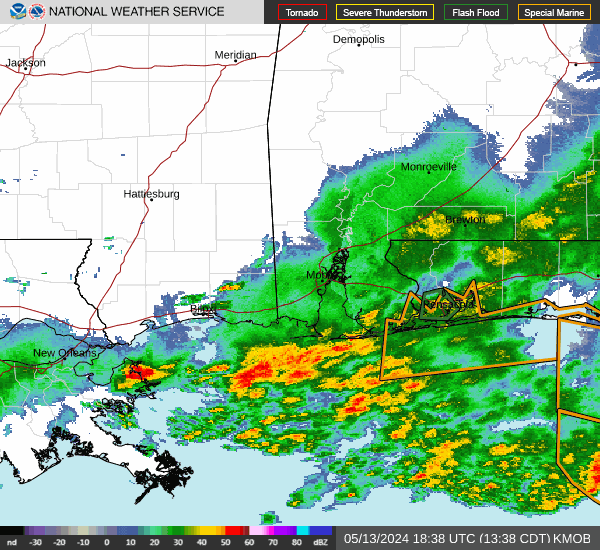
If you've posted on any weather forum or ever looked at models you've seen a chart that looks like this:

It's a go to to quickly give a tremendous amount of information, but it is worth knowing why this map tells us so much.
All the geopotential is telling you is the amount of work required to lift some mass from the ground to a certain height above the ground against the force of gravity. We assume gravity is roughly constant in the lower levels of the atmosphere where we live, so it's basically just telling you how high above the ground a given pressure level is.
Easy enough, but why does that matter?
It can tell us the wind speed and direction in the larger scale flow, explain why the jet stream is a thing, inform us about cold or warm air advection (warm or cold air moving horizontally), and explain my user name.
Now for the math.
We'll call the Geopotential Height "Z"
We can also find the thickness between two pressure levels, which is the difference in geopotential height from the lower pressure level to the top.
Let's call the thickness dZ. or "difference in geopotential heights (Z)
Through some math things I will spare you from: dZ = ((Rd * T) / g ) * ln (Plower / Pupper)
T is virtual temperature (just take this to mean average temp through the slice of air in question)
Rd is the Specific Gas Constant for dry air (it's like the R in PV = nRT, but specific to air)
g is the acceleration due to gravity (9.8 m/s^2)
P is pressure
Since g and Rd are constant, and we define the pressure levels what this tells you is that the thickness is a function of the temperature of the slice of air. Greater the thickness value, warmer it is.
The thickness between the surface and the 500 mb level is also going to basically be the geopotential height at 500 mb for most locations. So, the heights you see are related to temperature and the colors on the anomolies are telling you how relatively warm or cold the airmass is relative to normal.
Why the hell would that tell us about the wind speed and direction of the overall flow?
Ok, so assume there' s no acceleration happening to the wind. This holds on the larger time scales and length scales.
We can use this assumption to much more easily solve the complicated momentum equations.
For wind speed in a given direction (we'll use x-direction) you get: ug = - (1/(density * Coriolis force) * (change in pressure / change in y-direction)
Density is kind of a nasty term in this, because it varies with temperature and pressure and this equation considers change in pressure too. Not a whole lot of fun to solve.
But we can get around that, and this is where our Geopotential Height (Z) comes in handy.
Doing some calculus, we can eliminate density from the above equation and make it a function of the change in geopotential height / change in some direction.
This means we can say the wind speed in a given direction (x-direction) is: ug = - (gravity / Coriolis force) * (change in Z / change in y-direction)
What this says is the closer the height lines on the chart, the higher the wind speed is in that area.
And since wind speed has a lot to do with the pressure gradient, it tells you about the pressure gradient in an area. Which is why lower heights are called "upper lows" and higher heights "upper highs". Also where the terminology "trough" for lower heights and "ridge" for higher heights comes from, just like when looking at a topographical map.
That's it for post 1, but you can see how the heights are connected to both the temperature profile of the airmass and the larger scale wind speeds and direction.
Post 2, coming tomorrow night will get into the Thermal Wind!!!!!!! and why the polar jet stream is a thing.
If you've posted on any weather forum or ever looked at models you've seen a chart that looks like this:

It's a go to to quickly give a tremendous amount of information, but it is worth knowing why this map tells us so much.
All the geopotential is telling you is the amount of work required to lift some mass from the ground to a certain height above the ground against the force of gravity. We assume gravity is roughly constant in the lower levels of the atmosphere where we live, so it's basically just telling you how high above the ground a given pressure level is.
Easy enough, but why does that matter?
It can tell us the wind speed and direction in the larger scale flow, explain why the jet stream is a thing, inform us about cold or warm air advection (warm or cold air moving horizontally), and explain my user name.
Now for the math.
We'll call the Geopotential Height "Z"
We can also find the thickness between two pressure levels, which is the difference in geopotential height from the lower pressure level to the top.
Let's call the thickness dZ. or "difference in geopotential heights (Z)
Through some math things I will spare you from: dZ = ((Rd * T) / g ) * ln (Plower / Pupper)
T is virtual temperature (just take this to mean average temp through the slice of air in question)
Rd is the Specific Gas Constant for dry air (it's like the R in PV = nRT, but specific to air)
g is the acceleration due to gravity (9.8 m/s^2)
P is pressure
Since g and Rd are constant, and we define the pressure levels what this tells you is that the thickness is a function of the temperature of the slice of air. Greater the thickness value, warmer it is.
The thickness between the surface and the 500 mb level is also going to basically be the geopotential height at 500 mb for most locations. So, the heights you see are related to temperature and the colors on the anomolies are telling you how relatively warm or cold the airmass is relative to normal.
Why the hell would that tell us about the wind speed and direction of the overall flow?
Ok, so assume there' s no acceleration happening to the wind. This holds on the larger time scales and length scales.
We can use this assumption to much more easily solve the complicated momentum equations.
For wind speed in a given direction (we'll use x-direction) you get: ug = - (1/(density * Coriolis force) * (change in pressure / change in y-direction)
Density is kind of a nasty term in this, because it varies with temperature and pressure and this equation considers change in pressure too. Not a whole lot of fun to solve.
But we can get around that, and this is where our Geopotential Height (Z) comes in handy.
Doing some calculus, we can eliminate density from the above equation and make it a function of the change in geopotential height / change in some direction.
This means we can say the wind speed in a given direction (x-direction) is: ug = - (gravity / Coriolis force) * (change in Z / change in y-direction)
What this says is the closer the height lines on the chart, the higher the wind speed is in that area.
And since wind speed has a lot to do with the pressure gradient, it tells you about the pressure gradient in an area. Which is why lower heights are called "upper lows" and higher heights "upper highs". Also where the terminology "trough" for lower heights and "ridge" for higher heights comes from, just like when looking at a topographical map.
That's it for post 1, but you can see how the heights are connected to both the temperature profile of the airmass and the larger scale wind speeds and direction.
Post 2, coming tomorrow night will get into the Thermal Wind!!!!!!! and why the polar jet stream is a thing.